Represented while preserving its original size. By connecting the area of a circle to the area of a parallelogram, students can establish meaningful connections to their prior study of area of parallelograms in 6.G.1. The learning map section for this sequence of activities includes prerequisite knowledge of length, perimeter, and the ability to represent and solve equations. Building on an understanding of length, students can learn to explain diameter and radius. An understanding of perimeter provides the foundation for students to explain circumference.
Ask students what the base of the parallelogram would be related to the original circle. Questions could include, "Can you describe where the circumference of the circle falls on the decomposed circle? " and, "If the whole circumference is represented somewhere in this image, what fraction of the circumference falls here ? " Note that as the sectors get smaller, the shape gets closer and closer to a rectangle.
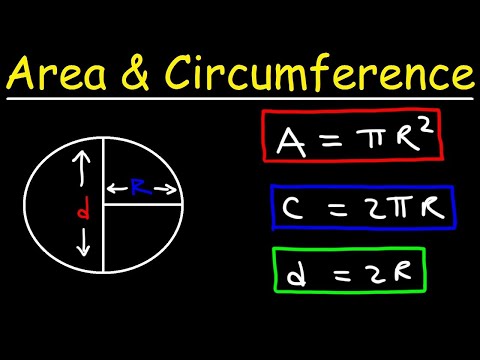
Remind students what the formula is for area of a parallelogram, and use this to derive the formula for the area of a circle. An example process is shown following this paragraph. The formula for the area of a circle is given by 𝜋 r2, where r is the radius of the circle. The value of 𝜋, pronounced pi, is 22/7 or 3.14. Pi is the ratio of the circumference to the diameter of a circle. It is one of the widely used mathematical constants.
The area of the circle is measured in terms of square units. Whatever be the unit of the radius, diameter or circumference, the same will be for the area of the circle but in terms of squares. The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle.
Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r.
The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle. A circle is a two-dimensional shape, it does not have volume. A circle only has an area and perimeter/circumference.
Let us learn in detail about the area of a circle, surface area, and its circumference with examples. The formula for the area of a circle helps us calculate the area of circle sectors and segments as well. A circle sector's area in relation to the area of the whole circle is much like that between an arc and the circumference. A sector bound by a central angle of n degrees is equal to (n/360) times the area of the circle. Why is the area of a circle pi times the square of the radius?
The usual definition of pi is the ratio of the circumference of a circle to its diameter, so that the circumference of a circle is pi times the diameter, or 2 pi times the radius. The animation above shows that a circle can be cut and rearranged to closely resemble a parallelogram of area pi times the square of the radius. By dividing the circle into more than eight slices, the approximation obtained in this manner would be even better. By dividing the circle into more and more slices, the approximating parallelograms approximate the area of the circle arbitrarily close. This give a geometric justification that the area of a circle really is "pi r squared".
It is easy to go from the area of a triangle to the area of a regular polygon by breaking the polygon into triangles and summing the areas of the triangles. But we need to first review the formula for the area of a polygon for reference. It can be shown that every regular polygon can be inscribed in a circle.
If we draw a perpendicular line from the center of the circle to any side of the inscribed polygon, that line is called an apothem. It is a fact that the area of a regular polygon is $1/2ap$ where $a$ is the apothem and $p$ is the perimeter of the polygon. It is also a fact that as the number of sides of the inscribed regular polygons increases, the lengths of the apothems of the polygons approach the radius of the circle. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14.
Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle. For example a 10 foot X 10 foot room equals 100 square feet. The area of a rectangle with sides of 5 units and 10 units equals 50 square units. You can therefore remember that the circle equation for area is the one that is squared.
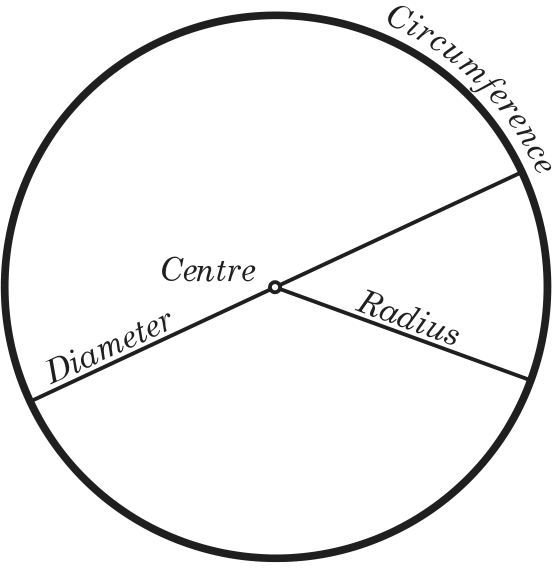
A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant. The word circle is derived from the Greek word kirkos, meaning hoop or ring. In this article, we cover the important terms related to circles, their properties, and various circle formulas. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point.
Basically, a circleis a closed curve with its outer line equidistant from the center. The fixed distance from the point is the radius of the circle. In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc.
Now let us learn, what are the terms used in the case of a circle. A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π. As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'.
The original proof of Archimedes is considered not rigorous by modern standards. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. Why is the formula to find the area of a circle 𝜋r²?
To derive the area of a circle formula, divide a circle into various triangles, such that these triangles can be joined in the form of a rectangle as shown in the figure. The more the number of sections, the more clear the rectangle shape will be. A circle is a closed curve formed by a set of points on a plane that are the same distance from its center. The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared. Circle is a collection of points that are at a fixed distance from a particular point.
Every line passing through the circle forms the line of reflection symmetry. In addition to this, it has rotational symmetry around the center for every angle. Some of the examples of circles are wheels, pizzas, circular ground, etc. The distance from the center to the circle is known as radius. Like all geometric shapes, circles take up space and a formula is required to calculate the area. A circle is known as a closed plane geometrical shape.
Technically, it is the locus of a point that moves around a fixed point at a fixed distance that is away from that point. A circle is basically a closed curve that has its outer line at an equal distance from the centre. This fixed distance from the central point is known as the radius of the circle. In our day to day life, we often see many examples like a pizza, wheel, etc.
Let us learn about these terms in regards to a circle. In this method, we divide the circle into 16 equal sectors. The sectors are arranged in such a way that they form a rectangle.
All sectors are similar in area, so hence all sectors' arc length would be equal. The circle's area would be the same as the area of the parallelogram shape or rectangle. Fill the circle with radius r with concentric circles.
After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. This area is the region that occupies the shape in a two-dimensional plane.
Now we will learn about the area of the circle. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. A circle is a collection of points that are at a fixed distance from the center of the circle.
We see circles in everyday life such as a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed inside the circle is known as the area of the circle. The base of the figure is represented by half the circumference of the circle, and the height of the figure is represented by the radius of the circle.
Therefore, using the formula for the area of a parallelogram, the area of a circle equals half the circumference times the radius. As the number of sides increases, the length of the parallelogram base approaches half the circle circumference and its height approaches half the circle radius. By this, the parallelogram turns into a rectangle with dimensions of width πr and height r. Use a protractor to measure the central angle made by the two radii. Set the base of the protractor along one of the radii, with the central point of the protractor aligned with the center of the circle.
Then read the angle measurement that corresponds with the position of the second radius forming the sector. The perimeter of a closed figure is known to be the length of its total boundary. When it comes to the circles, the perimeter is called by a different name. It is referred to as the 'circumference' of the given circle. This circumference is known as the total length of the boundary of the given circle. If we open the circle and form a straight line, the length of the straight line that we get is the circumference.
For defining the circumference of a circle, we need to know a term called 'pi'. Consider the circle shown below having its centre at O and radius r. In this method, the circle is divided into many small sectors and the arrangement of the sectors has been done in the form of a parallelogram as shown in the figure below. Clearly, if the circle is divided into more sectors, the parallelogram will turn into a rectangle.
When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area. A perimeter of closed figures is defined as the length of its boundary. When it comes to circles, the perimeter is given using a different name.
It is called the "Circumference" of the circle. This circumference is the length of the boundary of the circle. If we open the circle to form a straight line, then the length of the straight line is the circumference. To define the circumference of the circle, knowledge of a term known as 'pi' is required.
Observe the above figure carefully, if we split up the circle into smaller sections and arrange them systematically it forms a shape of a parallelogram. The more the number of sections it has more it tends to have a shape of a rectangle as shown above. For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. Ask students what they think would happen if they could cut the circle into an infinite number of sectors and arrange them in a similar fashion .
Ask students what they think is true about the area of this figure compared to the area of the original circle . Draw the radius on one of the sectors as shown in the following image . Ask students what measurement this would be, approximately, in a parallelogram . If students struggle to answer, you could draw in a parallelogram as shown in the following image to scaffold the question. The ratio of the distance around the circle to the diameter of the circle is defined as pi (π). Using the values in one row of your table, explain how the diameter, the distance around the circle, and pi are related mathematically.














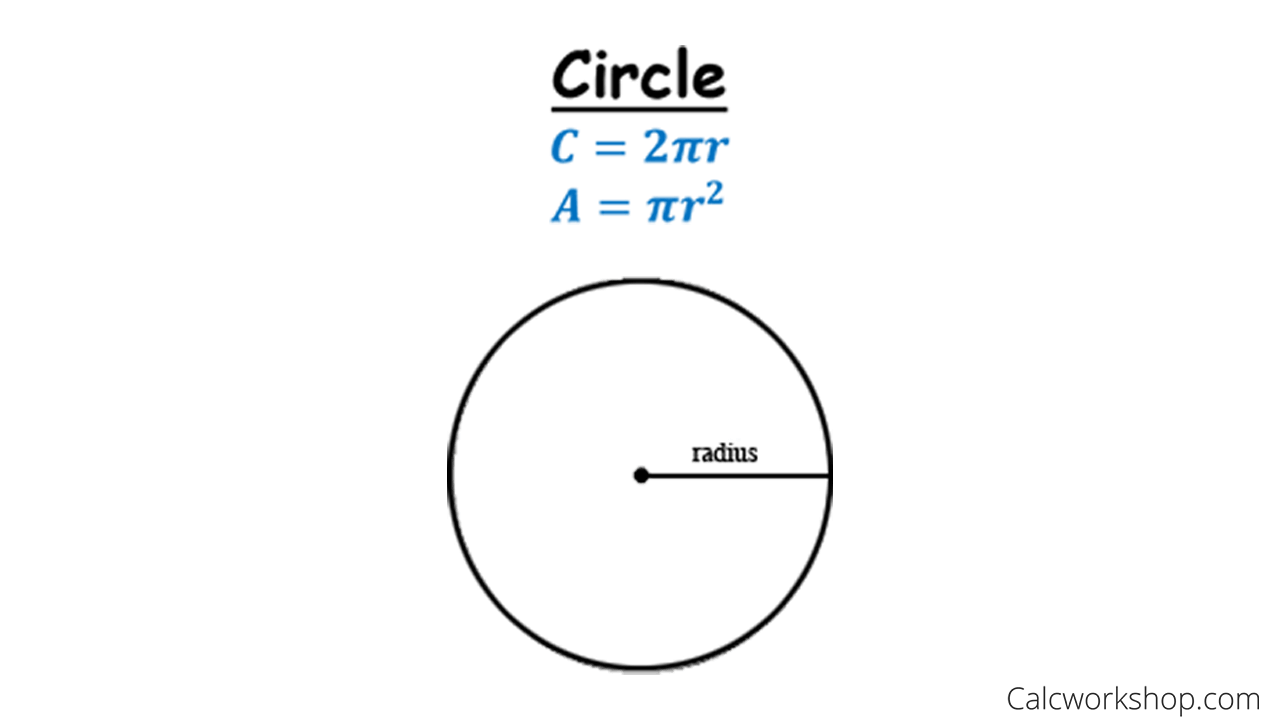










No comments:
Post a Comment
Note: Only a member of this blog may post a comment.